Inequalities

1. Crux Mathematicorum.Problem 4848.

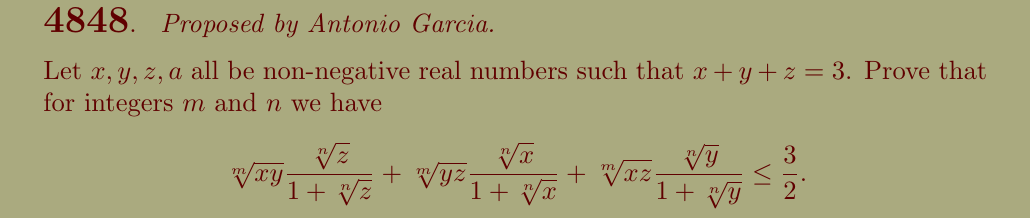
Supposons que \(x\geq y \geq z\). Nous avons que \(\sqrt[m]{xy}\geq \sqrt[m]{xz}\geq \sqrt[m]{yz}\) et \(\begin{equation} \frac{\sqrt[n]{x}}{1+\sqrt[n]{x}}\geq \frac{\sqrt[n]{y}}{1+\sqrt[n]{y}}\geq \frac{\sqrt[n]{z}}{1+\sqrt[n]{z}} \end{equation}\)

Par l’inégalité de Chebyshev, \(\begin{equation} \sum \sqrt[m]{xy} \frac{\sqrt[n]{z}}{1+\sqrt[n]{z}}\leq 1/3*(\sum \sqrt[m]{xy})(\sum \frac{\sqrt[n]{x}}{1+\sqrt[n]{x}}) \end{equation}\) Les dérivées secondes des functions \(\sqrt[m]{x}\) et \(\frac{\sqrt[n]{x}}{1+\sqrt[n]{x}}\) sont négatives. Donc les fonctions sont concaves. Alors par l’inégalité de Jensen, \(\begin{equation} \sum \frac{\sqrt[n]{x}}{1+\sqrt[n]{x}}\leq 3*\frac{\sqrt[n]{(x+y+z)/3}}{1+\sqrt[n]{(x+y+z)/3}}=3/2, \end{equation}\)

\(\begin{equation} \sum \sqrt[m]{xy}\leq 3*\sqrt[m]{(xy+xz+yz)/3} \end{equation}\) Mais on connaît que \(3(xy+xz+yz)\leq (x+y+z)^2=9\rightarrow xy+xz+yz\leq 3\) Par conséquent, \(\sum \sqrt[m]{xy} \frac{\sqrt[n]{z}}{1+\sqrt[n]{z}} \leq 1/3*3*3/2=3/2\)